Competitive Equilibrium
Oh, Hyunzi. (email: wisdom302@naver.com)
Korea University, Graduate School of Economics.
2024 Spring, instructed by prof. Koh, Youngwoo.
Basic Model
Consumers
Producers
- if
- if
- if
- set of feasible production plans.
- if
Allocation
- it is assumed that every resource belongs to someone.
Given
Ownership
- note that
Pareto Efficient Allocations
An feasible allocation
- Pareto Efficient does not concern with distributional issues.
An allocation
Note that the equalities hold at optimum since
- demand for good
where the second equality guarantees the unique
Let the allocation
Proof.Let
F.O.C.
Therefore,
- MRS for any goods
- MRTS for any goods
- MRS and MRTS for any goods
this completes the proof. □
Competitive Equilibrium
A feasible allocation
- Profit maximization:
- Utility maximization:
- Market clearing:
If
If
- Market clearing:
- Consumer's budget constraints:
then the market of good
Proof.From the market clearing condition, for all
Two-goods Economy
Suppose there are two goods (
- initial endowment:
- price of good
- consumer
- firm
Proof.let the price is given as
CE conditions:
- Profit maximization: for each
- Lagrangian
- F.O.C.
- if
- if
- if
- Lagrangian
- Utility maximization: for each
- Lagrangian:
- F.O.C.
- Lagrangian:
- Market clearing: by the ^2c4b14Theorem 7 (Walras law in CE), ISTS that the market clears for the good
Let
note that these conditions are determined independent to
AD function:
since
the Walrasian demand function for consumer
the Aggregate demand function is
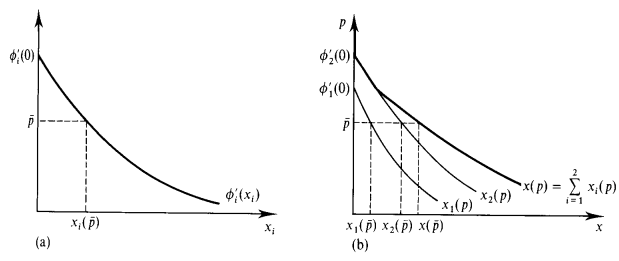
AS function:
since
the supply function for firm
the Aggregate supply function is
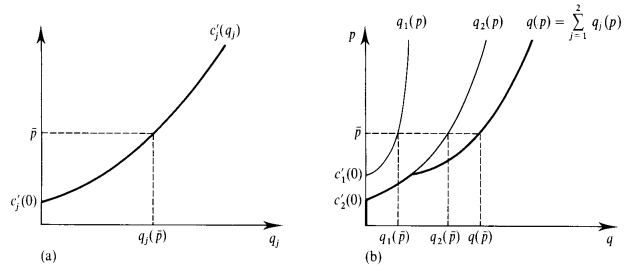
Equilibrium: at
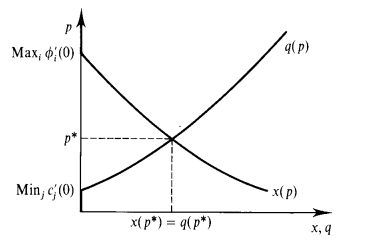
Note that
- Marginal Cost function:
- Marginal social benefit:
this completes the answer. □
Robinson Crusoe Economy
Robinson, who lives in a desert island, works in the daytime (Robinson producer; RP) and consumes "consumption" and "leisure" in the remaining time (Robinson consumer; RC).
- RC's initial endowment:
- RC's utility:
- RC is the only provider of labor: he owns the firm.
- RP's production function:
Proof.let
CE conditions:
- Profit maximization: RP solves,
- F.O.C:
- profit function:
- F.O.C:
- Utility maximization: RC solves,
- F.O.C:
- F.O.C:
- Market clearing: by letting
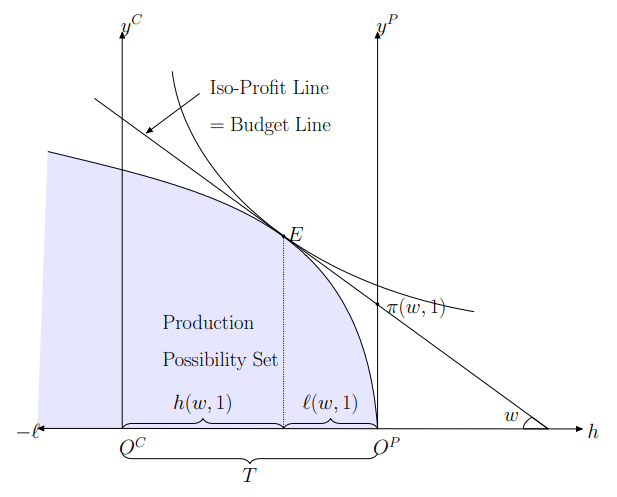
this completes the answer. □
Welfare Theorems
- FWT(CE
- complete set of market: every relevant good is traded in a market at publicly known prices.
- price takers: every households and firms act perfectly competitive.
- SWT(PE
- household preference and firm production sets are convex.
- markets are complete
- every agents are price takers
- appropriate lump-sum transfers of wealth are arranged
If
Proof.
RTA: suppose that
since it is not PE, there exists a feasible
therefore,
since CE is PMP & UMP, there exists no other feasible allocation that can strictly increases the utility.
Suppose that
Proof.Consider a hypothetical economy
- define
- let
- let
WTS#1:
- from
- since
- as
- thus,
- as
- then, since
- by letting
WTS#3:
At PE, there is no other feasible allocation that can strictly increase utility. Thus there exists some PE that is also CE, where we can achieve by rearranging the wealth by lump-sum treasfering.